الأعداد المركبة ( العقدية )
العدد العقدي أو العدد المركب هو أي عدد على الصورة:  حيث أن a و b هما عددان حقيقيان و i هو عدد تخيلي مربعه = -1. و يسمي العدد الحقيقي a بالجزء الحقيقي و العدد الحقيقي b بالجزء التخيلي. فمثلا، 3 + 2i هو عدد عقدي، فيه 3 هو الجزء الحقيقي، و 2 هو الجزء التخيلي.
حيث أن a و b هما عددان حقيقيان و i هو عدد تخيلي مربعه = -1. و يسمي العدد الحقيقي a بالجزء الحقيقي و العدد الحقيقي b بالجزء التخيلي. فمثلا، 3 + 2i هو عدد عقدي، فيه 3 هو الجزء الحقيقي، و 2 هو الجزء التخيلي.
و عندما يكون b (أي الجزء التخيلي) = 0، فإن قيمة العدد العقدي تساوي قيمة الجزء الحقيقي a فقط و سمي العدد عددًا حقيقيـًا صرفًا Purely real. و عندما يكون a (أي الجزء الحقيقي) = 0، كان العدد تخيليـًا صرفـًا Purely imaginary.
 حيث أن a و b هما عددان حقيقيان و i هو عدد تخيلي مربعه = -1. و يسمي العدد الحقيقي a بالجزء الحقيقي و العدد الحقيقي b بالجزء التخيلي. فمثلا، 3 + 2i هو عدد عقدي، فيه 3 هو الجزء الحقيقي، و 2 هو الجزء التخيلي.
حيث أن a و b هما عددان حقيقيان و i هو عدد تخيلي مربعه = -1. و يسمي العدد الحقيقي a بالجزء الحقيقي و العدد الحقيقي b بالجزء التخيلي. فمثلا، 3 + 2i هو عدد عقدي، فيه 3 هو الجزء الحقيقي، و 2 هو الجزء التخيلي.و عندما يكون b (أي الجزء التخيلي) = 0، فإن قيمة العدد العقدي تساوي قيمة الجزء الحقيقي a فقط و سمي العدد عددًا حقيقيـًا صرفًا Purely real. و عندما يكون a (أي الجزء الحقيقي) = 0، كان العدد تخيليـًا صرفـًا Purely imaginary.
من الممكن إجراء العمليات الحسابية العادية على الأعداد العقدية، كالجمع و الطرح و القسمة و الضرب، تمامًا كالأعداد الحقيقية، و لكنها أيضـًا تتمتع بخصائص أخرى تمكنها من حل كافة المعادلات الجبرية العادية التي يصعب حلها باستخدام الأعداد الحقيقية فقط.
و أحيانـًا قد يكتب العدد العقدي z على الصورة z = a + bj (خصوصـًا في مجال الهندسة الكهربية، لأن i هو رمز التيار الكهربي)
و أحيانـًا قد يكتب العدد العقدي z على الصورة z = a + bj (خصوصـًا في مجال الهندسة الكهربية، لأن i هو رمز التيار الكهربي)
تمثيل الأعداد المركبة
إذا فرضنا أن z هو عدد مركب، و a و b هما عددان حقيقيان، و i هو عدد تخيلي، فمن الممكن تمثيل العدد المركب z كما يلي:
إذا فرضنا أن z هو عدد مركب، و a و b هما عددان حقيقيان، و i هو عدد تخيلي، فمن الممكن تمثيل العدد المركب z كما يلي:
التمثيل الجبري
يكتب العدد المركب z جبريًا بالشكل: 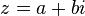
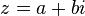
التمثيل الهندسي
يكتب العدد على شكل 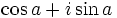
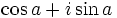
التمثيل الأسي
يكتب العدد على شكل 

فهم الأعداد العقدية
عندما وجد الرياضيون أن المعادلة (x2=-1)مستحيلة الحل في مجموعة الأعداد الحقيقية كان لا بد من أن يوضع لها حلاً وبما أن الرياضيات هي -وكما يقول أحد الرياضيين- العلم الذي لا نعرف فيه إن كان ما نوله صحيح أم لا. لذلك تم إيجاد عدد جديد هو العدد (تاء - ت )بالعربية وبلاتينية العدد(i)وتعريف العدد i هو الجذر التربيعي للعدد -1 .وهنا يكمن التعقيد فمن المعلوم انه ليس لعدد -1 جذر ولكن هذا في الأعداد الحقيقية فكما أنه لا وجود لعدد -5 في الأعداد الطبيعية ولكنه موجدود في الأعداد الصحيحة والحال نفسه بالنسبة لعدد i فالرياضيات هي علم وضعه البشر ولهم الحق في تطويرة وتجديدة وفق قواعد واضحة تضع للمنطق الرياضي لا تنافي المبادئ الرياضيةوالموضوعات والبديهيات في علم الرياضيات
الحساب في مجموعة الأعداد العقدية
الجمع
الجمع
تتم عملية الجمع كما يلي:
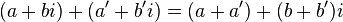
الضرب
تتم عملية الضرب كما يلي
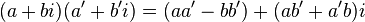
الخارج
تتم عملية القسمة كما يلي:

مرافق عدد عقدي
تعريف
تعريف
مرافق العدد العقدي  هو العدد العقدي
هو العدد العقدي  .
.
مرافق العدد العقدي z نرمز له ب:
 هو العدد العقدي
هو العدد العقدي  .
.مرافق العدد العقدي z نرمز له ب:

الأعداد المترافقة و العمليات
- مرافق مجموع عددين عقديين هو مجموع مرافق كل من حدي المجموع
- مرافق جداء عددين عقديين هو جداء مرافق كل من حدي الجداء
معيار عدد عقدي
جدر مربع جداء عدد عقدي في مرافقه يسمى معيار العدد العقدي
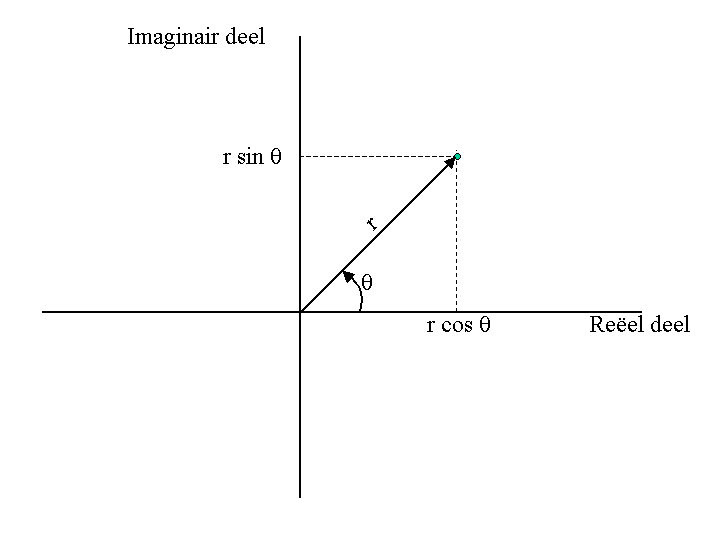
التمثيل الهندسي للأعداد العقدية
لحق نقطة
لحق نقطة
المستوى 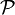 منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالنقطة M من
منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالنقطة M من 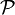 التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي
التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي  يسمى 'لحق' النقطة M.
يسمى 'لحق' النقطة M.
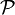 منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالنقطة M من
منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالنقطة M من 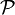 التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي
التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي  يسمى 'لحق' النقطة M.
يسمى 'لحق' النقطة M.لحق متجهة
المستوى المتجهي 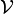 منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالمتجهة
منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالمتجهة 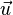 من
من 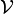 التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي
التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي  يسمى 'لحق' المتجهة
يسمى 'لحق' المتجهة 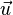 .
.
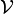 منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالمتجهة
منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالمتجهة 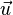 من
من  التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي
التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي  يسمى 'لحق' المتجهة
يسمى 'لحق' المتجهة 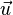 .
.
ليست هناك تعليقات:
إرسال تعليق