توحيد المقامات هو مفهوم رياضي لتسهيل جمع أو طرح الكسور، الفكرة الأساسية من وراءه تتمثل في أن جمع أي كسرين يمكن تبسيطه عن طريق إشتراك الكسرين بذات المقام، وهو الأمر الذي يعني ببساطة الحديث عن نفس الوحدة عند جمع البسط. فمثلا، الأنصاف والأرباع يمكن جمعها عند توحيد القيم المراد جمعها على أنها أرباع، وذلك بمضاعفة عدد الأنصاف لدى تحولها إلى أرباع، فمجموع النصف والربع هو عبارة عن مجموع الربعين والربع، حيث كل نصف هو عبارة عن ربعين. في المستوى النظري، لا يهم ما هي القيم التي يتم ضرب الكسور بها من أجل الوصول إلى مقامات مشتركة، لكن على المستوى العملي، فإن الطريقة الأسهل للوصول إلى مقامات موحدة هي ضرب كل من البسط والمقام لكل كسر بمقام الكسر الآخر، مما ينتج عنه عدد مشترك في المقام، وبالتالي تصبح عملية جمع الكسور لا تحتاج أكثر من جمع قيم البسط (الناتجة بعد الضرب في المقام الآخر) واستخدام المقام الموحد. مثال
إظهار الرسائل ذات التسميات amany. إظهار كافة الرسائل
إظهار الرسائل ذات التسميات amany. إظهار كافة الرسائل
الجمعة، 26 نوفمبر 2010
عدد كسري
الأعداد الكسرية هي نسبة عددين صحيحين إلى بعضهما وعادة ما تكتب بالشكل : أ/ب أو a/b وتدعى كسر، حيث ب لا تساوي الصفر، ندعو أ أو a الصورة أو البسط، وندعو ب أو b المخرج أو المقام.
يمكن كتابة أي عدد كسري بعدد غير منتهي من الأشكال (كنتيجة عن خواص التناسب): 3 / 6 = 2 / 4 = 1 / 2. ويعتبر الشكل أبسط ما يكون عندما لا يكون للبسط (الصورة) والمقام (المخرج) أي قواسم مشتركة (في المثال السابق : 1 / 2).
يمكن أيضا التعبير عن أي عدد كسري بشكل كسر عشري ويكون الكسر العشري الممثل للعدد الكسري دوري أو يمكن القول (دوريًا)(أي أن الأرقام الموجودة في الكسر العشري تتكرر بشكل دوري : 0.234234234، 12.363636، 452.563256325632). وهنا يستخدم رمز الخط العلوي للتعبير عن هذه الأعداد الكسرية الدورية.
بالمقابل توجد مجموعة من الأعداد الحقيقية لا تمتلك صفة الدورية هذه في الكسر العشري ولا يمكن التعبير عنها بنسبة عددين صحيحين : وهذه تدعى بالأعداد غير المنطقة أو غير الكسرية (بالإنجليزية: irrational number).
يمكن كتابة أي عدد قياسي بعدد غير منتهي من الأشكال (كنتيجة عن خواص التناسب): 3 / 6 = 2 / 4 = 1 / 2. ويعتبر الشكل أبسط ما يكون عندما لا يكون للبسط (الصورة) والمقام (المخرج) denominator أي قواسم مشتركة (في المثال السابق : 1 / 2).
مجموعة الأعداد القياسية - ويرمز لها بالرمز - هي مجموعة جزئية من مجموعة الأعداد الحقيقية وتحوي مجموعة الأعداد الصحيحة، أي أن
- هي مجموعة جزئية من مجموعة الأعداد الحقيقية وتحوي مجموعة الأعداد الصحيحة، أي أن  . وتكون مجموعة الأعداد القياسية حقلاً مرتبًا أرشميديًا.
. وتكون مجموعة الأعداد القياسية حقلاً مرتبًا أرشميديًا.
من الحقائق المعروفة أيضًا عن الأعداد القياسية:
العمليات الحسابية يكون عددان كسريان
يمكن كتابة أي عدد كسري بعدد غير منتهي من الأشكال (كنتيجة عن خواص التناسب): 3 / 6 = 2 / 4 = 1 / 2. ويعتبر الشكل أبسط ما يكون عندما لا يكون للبسط (الصورة) والمقام (المخرج) أي قواسم مشتركة (في المثال السابق : 1 / 2).
يمكن أيضا التعبير عن أي عدد كسري بشكل كسر عشري ويكون الكسر العشري الممثل للعدد الكسري دوري أو يمكن القول (دوريًا)(أي أن الأرقام الموجودة في الكسر العشري تتكرر بشكل دوري : 0.234234234، 12.363636، 452.563256325632). وهنا يستخدم رمز الخط العلوي للتعبير عن هذه الأعداد الكسرية الدورية.
بالمقابل توجد مجموعة من الأعداد الحقيقية لا تمتلك صفة الدورية هذه في الكسر العشري ولا يمكن التعبير عنها بنسبة عددين صحيحين : وهذه تدعى بالأعداد غير المنطقة أو غير الكسرية (بالإنجليزية: irrational number).
صفات الأعداد الكسرية
العدد القياسي أو الكسري أو هو ما يمكن كتابته ككسر إعتيادي أو خارج قسمة عدد صحيح على عدد صحيح موجب. وعادة ما تكتب بالشكل : أ / ب أو a/b حيث ب لا تساوي الصفر، ندعو أ أو a الصورة أو البسط، وندعو ب أو b المخرج أو المقام.يمكن كتابة أي عدد قياسي بعدد غير منتهي من الأشكال (كنتيجة عن خواص التناسب): 3 / 6 = 2 / 4 = 1 / 2. ويعتبر الشكل أبسط ما يكون عندما لا يكون للبسط (الصورة) والمقام (المخرج) denominator أي قواسم مشتركة (في المثال السابق : 1 / 2).
مجموعة الأعداد القياسية - ويرمز لها بالرمز
 - هي مجموعة جزئية من مجموعة الأعداد الحقيقية وتحوي مجموعة الأعداد الصحيحة، أي أن
- هي مجموعة جزئية من مجموعة الأعداد الحقيقية وتحوي مجموعة الأعداد الصحيحة، أي أن  . وتكون مجموعة الأعداد القياسية حقلاً مرتبًا أرشميديًا.
. وتكون مجموعة الأعداد القياسية حقلاً مرتبًا أرشميديًا.من الحقائق المعروفة أيضًا عن الأعداد القياسية:
- أي عدد قياسي هو عدد جبري (أي حل لمعادلة جبرية معاملاتها أعداد صحيحة).
- أي عدد قياسي له تمثيل عشري منتهي أو دوري.
- وبالعكس أي عدد له تمثيل عشري منتهٍ أو دوري يكون بالضرورة عددًا قياسيًا.
العمليات الحسابية يكون عددان كسريان  و
و متساويان فقط وفقط إذا كان ad = bc.
متساويان فقط وفقط إذا كان ad = bc.
يتم جمع عددين كسريين كما يلي:

وتتم عملية الضرب كما يلي:
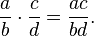
كما يوجد أيضًا المقلوب الجمعي والجدائي في الأعداد الكسرية كما يلي:


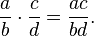

الاشتراك في:
الرسائل (Atom)

